Recap

In my previous post on functional programming features for “control flow”, I provided an overview of function composition, and discussed the use of higher-order functions and recursion as a form of “functional iteration”.

In this post, we will explore more on higher-order functions and how they can be used in designing functional data pipelines.

Before that, let’s start with how a typical data pipeline looks like.

Data Processing and the Data Pipeline Design Pattern

A classic approach to data processing is to write a program that uses the data pipeline design pattern.

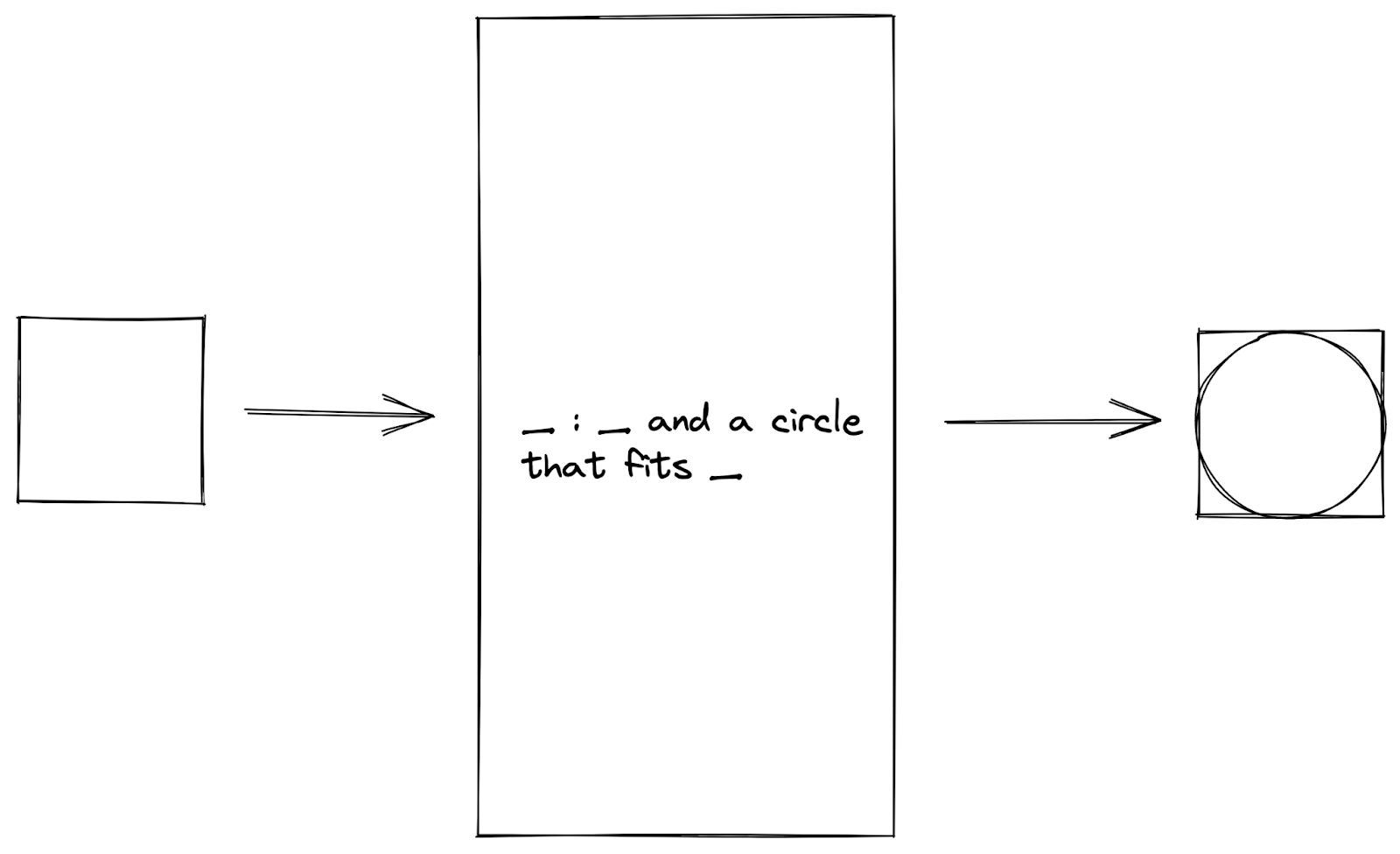Data Pipeline Design Pattern

In a typical data pipeline, we read data from a source, transform the data in some desired way, and collect the output as new data. This is what is commonly known as the “extract, transform, load” (ETL) process.

• Extract: In the data extraction phase, data is extracted from the source system(s) and validated for correctness.
• Transform: In the data transformation phase, a series of functions are applied to the extracted data in order to prepare it for loading to the target data store.
• Load: In the data load phase, the data is loaded into the target data store - it could be a flat file (such as CSV or Parquet) or data warehouse.

Higher-Order Functions for Data Transformations

A simplified sketch of a typical ETL process from database source to flat file in S3 bucket is shown below:

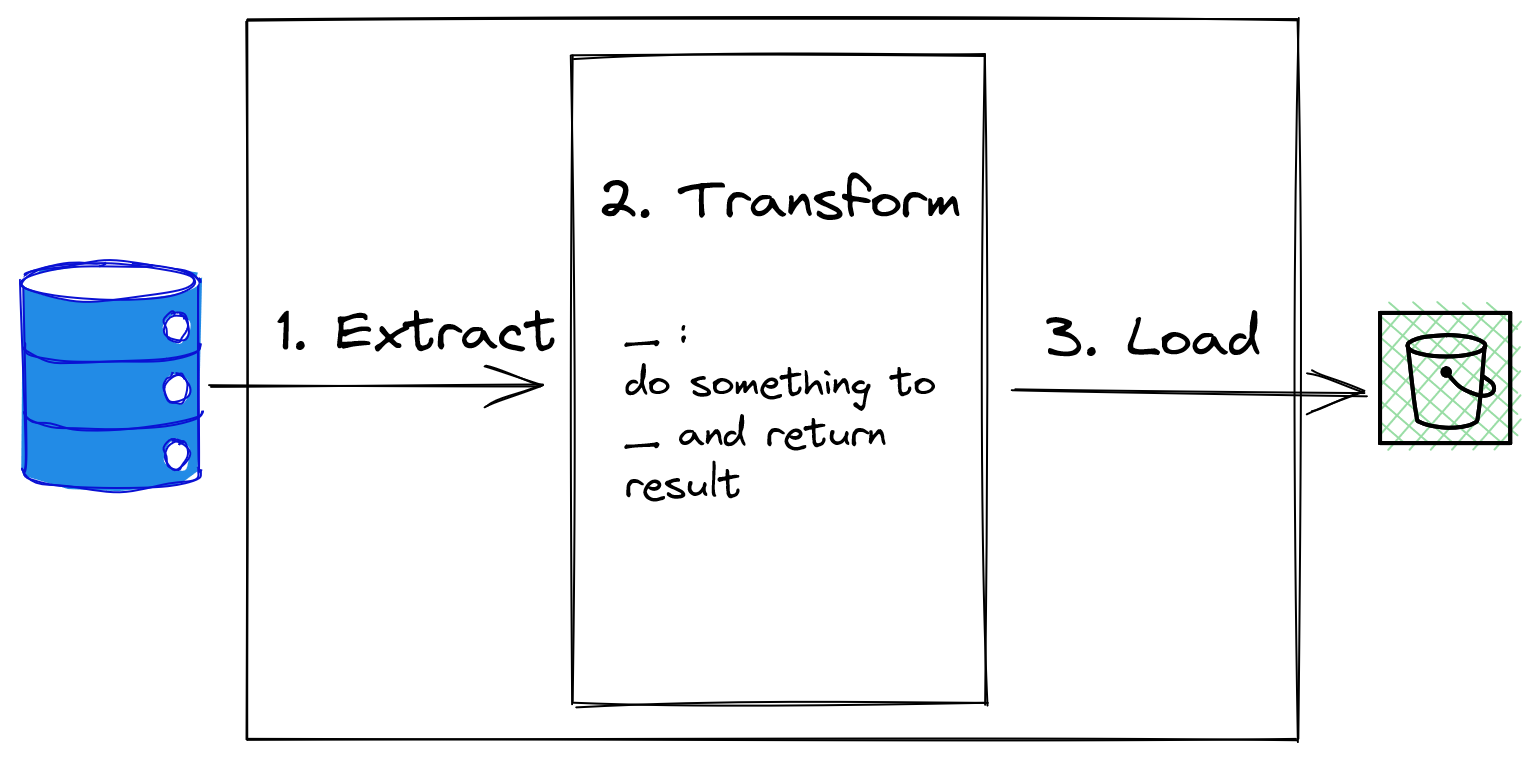Sketch of an ETL Process

While the data extraction and data load phases depend on the states of the source and target data store outside the program, the data transformation phase depends on the input data and the function applied to the data within the program itself. Hence, data transformation can be naturally expressed as a functional operation composed with a series of functions - also known as function composition.

For programming languages that support functions as first-class objects, function composition can be expressed in the form of a higher-order function. While we can write our own higher-order functions, there are a few useful built-in higher-order functions that are commonly used in data transformations:

• map
• filter
• reduce

The focus of this post is to explore these built-in higher-order functions and discuss how they can be used in designing functional data pipelines.

map

The map function accepts a function as input, applies the function to every element in a collection of values, and returns a new collection of function output values.

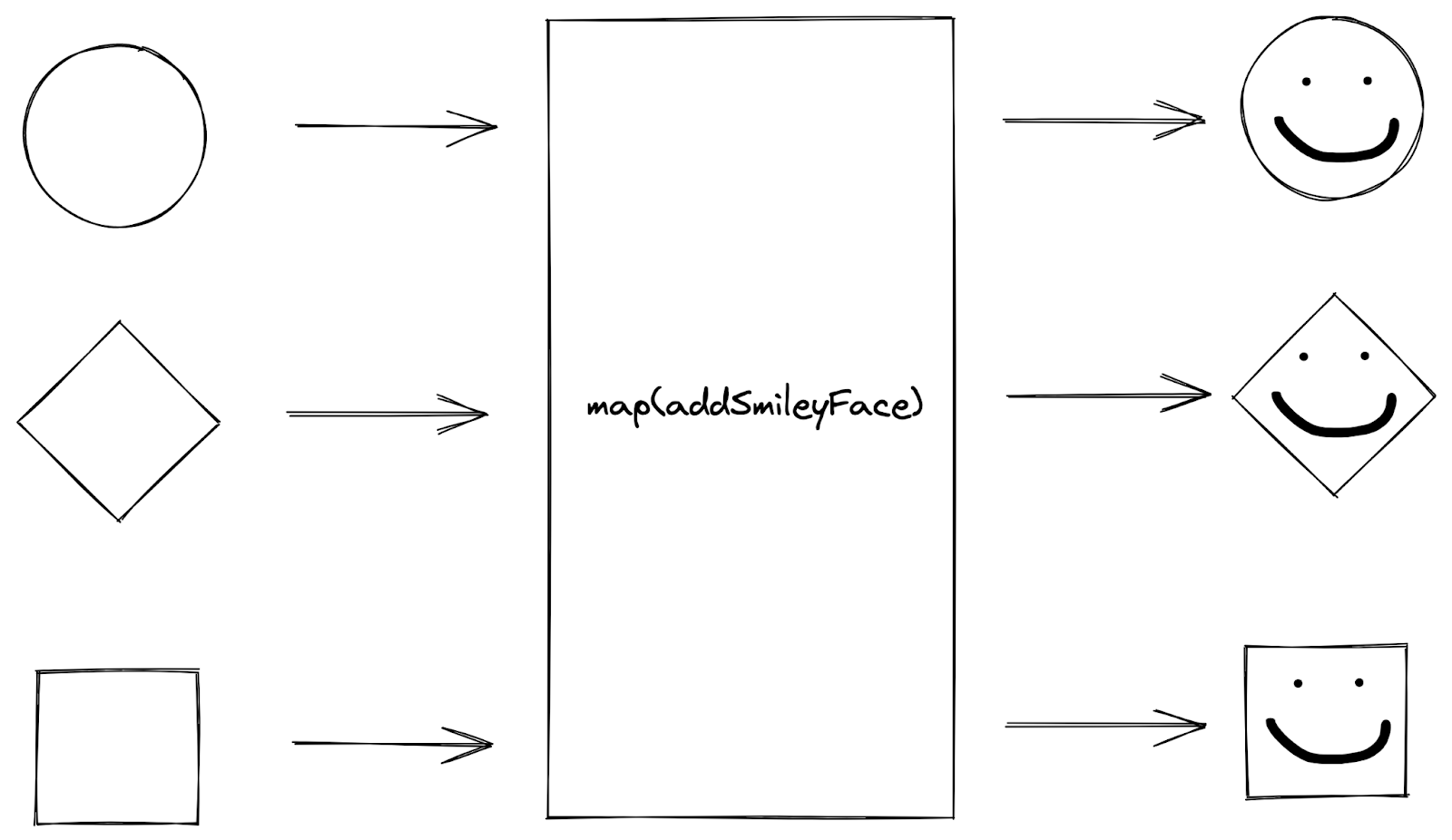Sketch of map function

For example, when we map a collection of shapes with an addSmile operation, we “map” each shape in the collection by applying the operation to the shape. The outputs from mapping the shapes with the addSmile operation are consolidated into a new collection of shapes with a smile added to the input shape.

A detailed discussion on the map implementation in Python and Scala can be found in my previous post.

filter

The filter function accepts a function that returns a boolean value (also known as a predicate) as input, applies the function to every element in a collection of values, and returns the elements that return true from the function as a new collection.

The predicate should accept a parameter of the same type as the elements in the collection, evaluate the result with the element, and return true to keep the element in the new collection or false to filter it out.

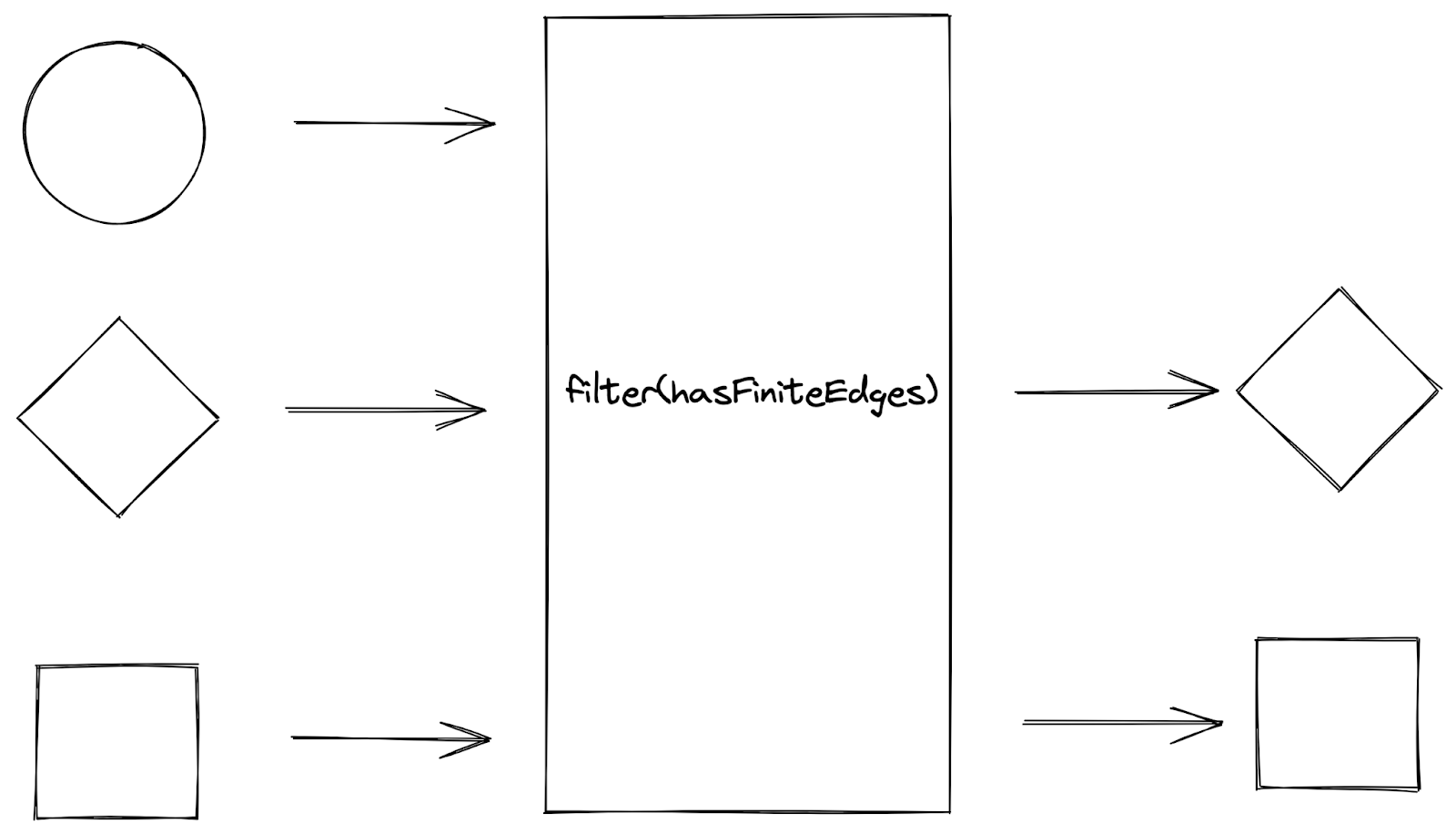Sketch of filter function

For example, when we apply the hasFiniteEdges condition to a collection of shapes, we “filter” each shape in the collection according to whether it satisfies the hasFiniteEdges condition. The shapes that returns true from the hasFiniteEdges function are consolidated into a new collection of shapes, with the shapes that do not satisfy the condition filtered out from the collection.

When we look at the documentation for the Python built-in function filter, it is stated that the filter function takes in a predicate function and an iterable as input parameters, and constructs an iterator from those elements of the iterable for which the predicate function returns true [1].

In Scala, each of the collection classes in package scala.collections and its subsets contain the filter method that is defined by the following function signatures on ScalaDoc [2]:

def filter(p: (A) => Boolean): Iterable[A]    // for collection classes
def filter(p: (A) => Boolean): Iterator[A]    // for iterators that access elements of a collection

What the function signatures mean is that filter takes a predicate input parameter p which transforms a generic input of type A to a Boolean value, and returns a new iterator consisting of all elements of the iterable collection (of type A) that satisfy the predicate p.

To create a new collection of even numbers from an existing collection of numbers using a functional approach, the filter function can be used to filter out the odd numbers from the collection by applying an even predicate to each element and collecting the elements that satisfy the even predicate condition into a new collection.

• In Python:

    def isEven(x):
        return x % 2 == 0
  
    def main(args):
  
        collection = [1,2,3,4,5]
        evenNums = list(filter(isEven, collection))
        print(evenNums)   
  

• In Scala:

    object FilterEven {
  
        def isEven(x: Int): Int = {
            x % 2 == 0
        }
  
        def main(args: Array[String]) {
  
            val collection = List[1,2,3,4,5]
            val evenNums = collection.filter(isEven)
            println(evenNums)
        }
    }    
  

In both implementations, the filter function accepts an input predicate that is applied to each element in a collection of values and returns a new collection containing the elements that satisfy the predicate.

reduce

The reduce function accepts a combining function (usually a binary operation) as input, applies the function to successive elements in a collection of values, and returns a single cumulative result.

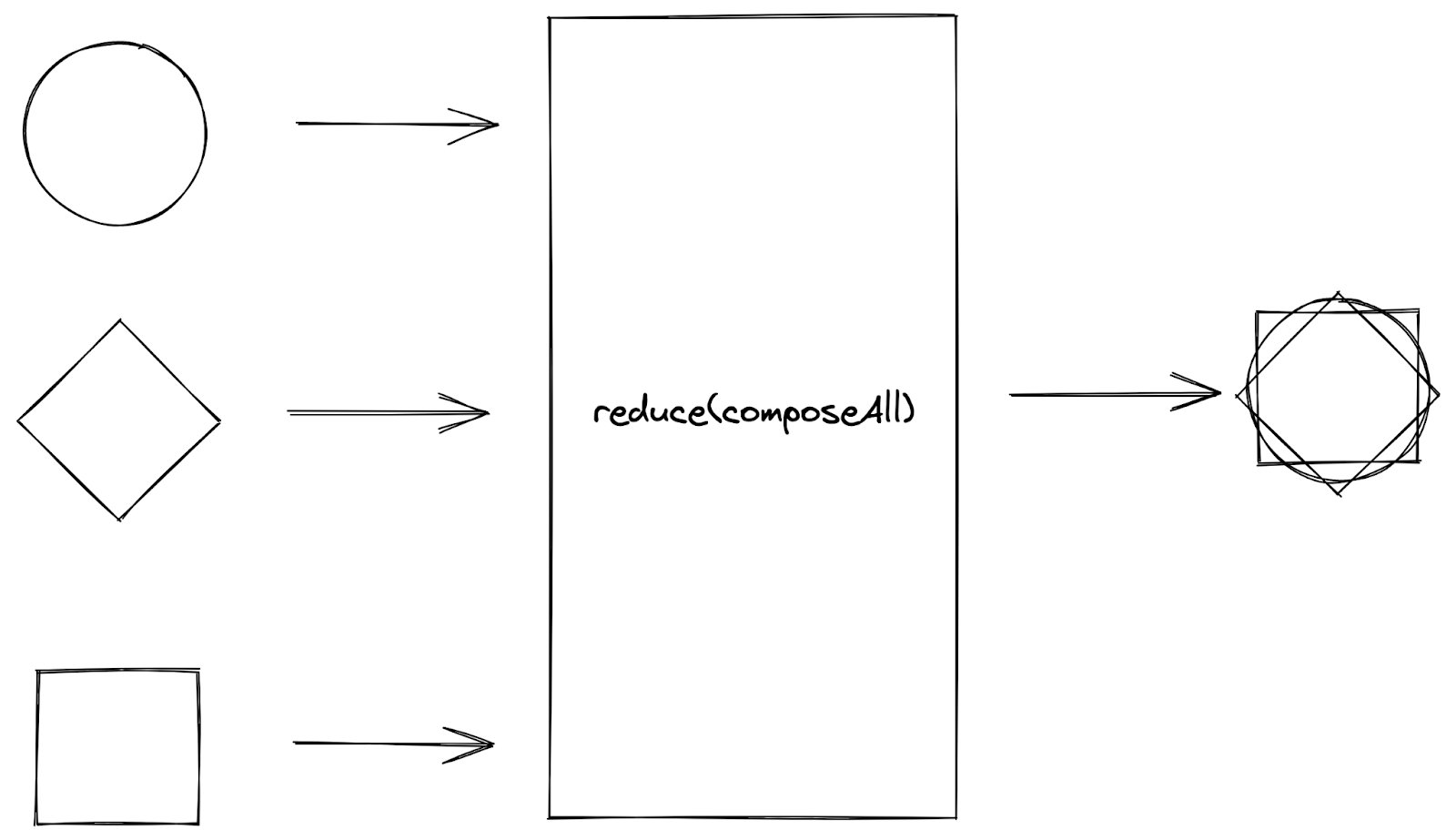Sketch of reduce function

For example, when we apply the composeAll operation to a collection of shapes, we “reduce” the shapes in the collection into a single result by folding a partial result and the shape in the iteration into a single result using the composeAll operation and using the composed result as the partial result for the next iteration. At the end of the iteration, the output from reducing the shapes with the composeAll operation is returned as a single result (of a composite of shapes).

When we look at the documentation for the Python reduce function in the functools library, it is stated that the reduce function takes in a function with two arguments and an iterable (with an optional initial value that can be placed before the items of the iterable in the calculation) as input parameters, and applies the function cumulatively to the items of an iterable from left to right [3].

In Scala, each of the collection classes in package scala.collections and its subsets contain the reduce method that is defined by the following function signatures on ScalaDoc [2]:

def reduce(B >: A)(op: (B, B) => B): B

What the function signature means is that reduce takes a binary operator op of result type B (a supertype of type A) which transforms two elements in the collection into a value of type B, and returns the result of applying the operator between all elements (of type A) in the collection. It is necessary for the binary operator op to return the same data type A or the supertype of the type B stored in the collection, so that the reduce method can perform the subsequent operation on the result of the operation and the next element in the collection that the operation is being applied on.

A closer look at the ScalaDoc for the reduce method indicates the following operating conditions:

1. The binary operator must be associative.
2. The order in which operations are performed on elements may be non-deterministic.

The associative property for the binary operator is a necessary condition to ensure that the order in which operations are performed during the reduction does not change the result for different runs - as long as the sequence of the elements being operated on is not changed.

While the associative property is necessary for returning a deterministic result from the reduction function (a necessary condition for referential transparency), it is not a sufficient condition as the order of operations can yield different results in the case of non-commutative binary operators such as subtraction and division.

What if we would like to specify the order of the operations to be performed on the elements of the collection?

In Scala, we have the reduceLeft and reduceRight methods in the collection classes which apply a binary operator cumulatively to all elements in the collection in left-to-right and right-to-left order respectively. The reduceLeft and reduceRight methods are defined by the following function signatures on ScalaDoc:

def reduceLeft[B >: A](op: (B, A) => B): B
def reduceRight[B >: A](op: (A, B) => B): B

The key differences between the function signatures for reduceLeft and reduceRight methods compared with the function signature for reduce are:

1. The binary operator op of result type B (a supertype of type A) takes the partial result (of type B) and the next element in the collection (of type A) and reduces them into a value of type B.
2. The order of the partial result and the element in the collection in the binary operation indicates the direction of operator application along the collection.

To obtain the cumulative sum of collection of numbers using a functional approach, the reduce function can be used to reduce a collection of numbers into a single value by applying the addition operator between consecutive numbers of the collection and performing the operation.

• In Python:

    def main(args):
  
        from functools import reduce
  
        collection = [1,3,5,2,4]
        totalSum = reduce(lambda x,y: x + y, collection)
        print(totalSum)   
  

• In Scala:

    object SumNumbers {
  
        def main(args: Array[String]) {
  
            val collection = List[1,3,5,2,4]
            val totalSum = collection.reduce((x, y) => x + y)
            println(totalSum)
        }
    }    
  

In both implementations, the reduce function accepts a binary operator that is applied between consecutive elements in a collection of values and returns a single result.

The left-to-right reduction (reduceLeft method in Scala) of the collection of numbers with the binary addition operator is evaluated in the following manner:

[1,3,5,2,4].reduceLeft((x, y) => x + y)    // initialize var acc = null
(((1 + 3) + 5) + 2) + 4    // take first value, acc = 1
((4 + 5) + 2) + 4    // acc = 1 + 3 = 5
(9 + 2) + 4  // acc = 4 + 5 = 9
11 + 4    // acc = 9 + 2 = 11
15    // acc = 11 + 4 = 15 returned upon end of collection

Similarly, the right-to-left reduction (reduceRight method in Scala) is evaluated in the following manner:

[1,3,5,2,4].reduceRight((x, y) => x + y)    // initialize var acc = null
1 + (3 + (5 + (2 + 4)))    // take first value from right, acc = 4
1 + (3 + (5 + 6))    // acc = 4 + 2 = 6
1 + (3 + 11))   // acc = 6 + 5 = 11
1 + 14   // acc = 11 + 3 = 14
15    // acc = 14 + 1 = 15 returned upon end of collection

As the addition operator is associative and commutative, the order of operator application does not affect the result and hence the reduce method can be safely used in the Scala implementation.

Notice the recursive pattern in how the addition operations are evaluated during the reduction? The reduce function is a special case of fold in functional programming, which refers to a family of higher-order functions that recursively combines elements in a recursive data structure into a single result.

The built-in collection methods sum, product, min, and max are defined based on the reduce function [4] with their corresponding binary operators:

While reduce function is useful for reducing a collection of values into a single value with associative binary operators, using these built-in collection methods in place of reduce could improve readability without reinventing the wheel for their intended use cases in data pipeline design.

Putting Them All Together

To summarize, built-in higher order functions are useful in constructing a sequence of data transformations within a data pipeline:

1. map for applying a function to all elements in a collection
2. filter for selecting elements in a collection based on a boolean condition
3. reduce for reducing a collection of elements into a single result with an associative operator between consecutive elements

While map and filter returns a new collection that can be processed with subsequent higher-order functions, reduce returns a single cumulative value. Hence, the reduce method and its derivatives are usually implemented as the final transformation step when designing functional data pipelines with function composition.

What’s Next

In this post, we learn about:

1. Data Pipeline design pattern
2. Higher-Order Functions for data transformation: map, filter, reduce

During our exploration on the map-filter-reduce trio of higher-order functions, we briefly mentioned two interesting concepts that are relevant to functional programming:

1. reduce as a special case of fold
2. collection classes as data containers with built-in methods

In the next few posts within the series, I will expand on these concepts and their applications in designing functional data pipelines.

References

1. Built-in Functions - Python 3.10.2 Documentation
2. Scala Standard Library 2.13.8 - scala.collections.Iterable
3. functools - Higher-order functions and operations on callable objects - Python 3.10.2 Documentation
4. trait IterableOnceOps - scala/IterableOnce.scala at v2.13.8